Vad kan vi lära av statistiskt signifikanta resultat?

Konventionen i många vetenskapliga discipliner är att ett p-värde på 5% tolkas som att ett resultat är statistiskt signifikant. Den replikeringskris som först uppstod inom psykologi, men nu tagit sig vidare till bland annat nationalekonomi, har dock visat att många statistiskt signifikanta resultat inte låter sig replikeras. En viktig orsak till detta är att tidskrifter framförallt publicerar statistiskt signifikanta resultat, vilket pressar forskare att medvetet eller omedvetet välja analysmetoder så att man tar sig under 5%-ribban (vilket fick mig att utfärda en varning för statistiskt signifikanta resultat här på Ekonomistas). Men en annan orsak att många resultat inte replikeras kan vara att ett p-värde på 5% helt enkelt är en alltför låg ribba för att betrakta ett resultat som statistiskt signifikant. Tyvärr misstänker jag att många tenderar att överskatta hur mycket vi bör tro på ett resultat som har ett p-värde på 5%.

Att det är lätt att misstolka vad ett p-värde på 5% betyder fick jag bittert erfara häromveckan när en kollega spände ögonen i mig i samband med ett mingel på institutionen och ställde följande fråga: Vad är oddsen är att det finns en verklig effekt om en experimentell studie redovisar ett p-värde på 5% och du innan studien trodde att det var lika sannolikt att det fanns en effekt som att det inte gjorde det? Svaret, som jag först hade svårt att tro på, är att oddsen maximalt är i storleksordningen 3 till 1.

Ett p-värde på 5% innehåller därför mindre information än det intryck många nog får när en effekt påstås vara ”vetenskapligt säkerställd”. Om man till exempel från början trodde att det var lika sannolikt att det finns en effekt som att det inte gör det, ska man alltså efter att ha observerat ett p-värde på 5% tro att sannolikheten att det finns en effekt är 75%. Om man från början var skeptisk, och kanske bara trodde att sannolikheten att det finns en effekt är 1 på 10, ska man efter att ha observerat ett p-värde på 5% bara tro att sannolikheten att det finns en effekt är som mest dryga 20%. För att reda ut varför det är på detta vis krävs dock att vi gräver lite djupare i vad ett p-värde egentligen betyder och tyvärr är resten av inlägget därför mer tekniskt än Ekonomistas-läsaren är van vid.

Förklaringen går tillbaka till den allra vanligaste misstolkningen av vad ett p-värde är, nämligen att p-värdet säger hur sannolikt det är att nollhypotesen är sann. Men som varje statistikstudent någon gång lärt sig säger p-värdet bara hur sannolikt det är att man får ett utfall som är minst lika extremt som det man observerar under antagandet att nollhypotesen stämmer. Ett exempel illustreras av den blå linjen i figuren nedan. Den blå linjen visar hur effektskattningar från hypotetiska experiment skulle vara fördelade om den sanna effekten vore noll. Om vi observerar ett p-värde på 5% i en studie innebär det att det observerade värdet ligger ganska långt ut i svansen av denna fördelning, vilket markeras av den streckade linjen i figuren. (För enkelhets skull visar jag ett enkelsidigt test.)

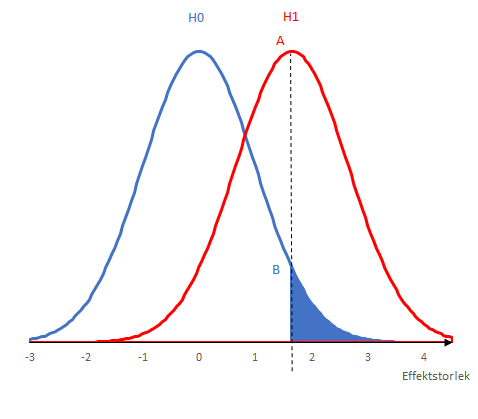P-värdet säger oss alltså bara hur sannolikt ett visst utfall är under antagandet att nollhypotesen är sann, medan det vi oftast vill veta är hur sannolikt det är att nollhypotesen stämmer. För att säga något om den saken måste vi specificera en alternativhypotes. Låt oss tänka oss ett extremfall då alternativhypotesen är att effekten är exakt så stor som den effekt vi observerade i experimentet. Om alternativhypotesen stämmer skulle den observerade effekten fördela sig enligt den röda kurvan i figuren ovan. För att avgöra hur sannolik nollhypotesen är måste vi även ställa oss frågan hur sannolikt det är att vi observerar ett p-värde på 5% om alternativhypotesen stämmer, vilket ges av punkten A i diagrammet ovan. För att räkna ut hur mycket mer trolig alternativhypotesen är relativt nollhypotesen måste vi därför dela värdet i punkten A med punkten B. I det här exemplet är den kvoten 3,9. Denna kvot kallas Bayes-faktorn och ska sedan multipliceras med förhandsoddsen för att alternativhypotesen är sann för att få rätt uppdaterad Bayesiansk uppfattning om hur sannolikt det är att det finns en effekt relativt att det inte gör det.

Vilka odds denna övning resulterar i beror på vad jag antagit om alternativhypotesen i mitt exempel. I mitt exempel valde jag dock alternativhypotesen så att kvoten mellan A och B blir så stor som möjligt. För mer rimliga alternativhypoteser som inte anger ett specifikt värde går det att visa att Bayes-faktorn med ett p-värde på 5% vid ett dubbelsidigt test inte kan bli större än 2,4-3,4. Figuren nedan illustrerar denna övre gräns under lite olika antaganden om alternativhypotesen för olika p-värden. Som visas i diagrammet nedan är Bayes-faktorn för ett p-värde på 1% betydligt högre än för 5%. För att dra rätt slutsats från en studie är det därför viktigt att inte bara tänka på om resultatet är statistiskt signifikant på 5%-nivån eller ej, utan vad det exakta p-värdet är.

Figuren ovan är hämtad från ett upprop i Nature Human Behavior där ett stort antal forskare, däribland professorn som läxade upp mig vid institutionsminglet, argumenterar för att tröskeln för att kalla en nyupptäckt effekt statistiskt signifikant bör sänkas från 5% till 0,5%. Huvudargumentet för detta är helt enkelt att p-värden uppemot 5% inte ger oss särskilt starka skäl att tro att det finns en effekt, i synnerhet inte då vi på förhand tror det är osannolikt att vi ska hitta en effekt.